Excelで簡単データサイエンス②「売上予測をレベルアップ！」

今回からは、実践編。初回のテーマは、売上予測のレベルアップです。
みなさんは、売上予測をどのように行っていますか？　飲食店であれば、気温・天気・周囲で行われるイベントの有無などから、売上予測を立てていると思います。

さてこの売上予測、精度は高いものでしょうか？　

精度がさらに上がり経営に生かすことができれば、売上の機会損失や在庫の余剰、原材料の廃棄や余分な人件費などが削減できるなどのメリットが期待できます。

１．売上予測には回帰分析を使おう

Excelで売上予測を立てる際には、『回帰分析』が有用です。回帰分析とは、データのある変数y（目的変数）の変動を、別の変数x（説明変数）の変動により説明・予測する手法です。

例えば、過去の売上データと日々の気温のデータがあれば、売上データを目的変数y、気温のデータを説明変数xと置くことで、気温が１℃上がれば売上が○○円上がる、といった関係性（以下、数式例）を見つけることができます。この数式の当てはまりが良い場合、予想気温から売上を定量的に推測することができるのです。

予測売上高：y（円）　＝　気温：ｘ（℃）　×　回帰係数：a　＋　定数：b

２．単回帰分析STEP1：データを視覚化する～散布図を作成～　

２つの変数の関係性を見たい場合、まずはデータを散布図で表し視覚的に関係性があるかを見る必要があります。
　

（１）データの準備

データの準備としては、関係性を見たい２つの変数をExcel上にプロットしたデータファイルを作成します。

データを準備する際には、目的変数を下、説明変数を上に並べることで、目的変数をy軸（縦軸）、説明変数をx軸（横軸）となるグラフを作ることができます。
（縦長でデータを準備する場合には、目的変数を右側に置くと、散布図にした際にy軸に表示できます）

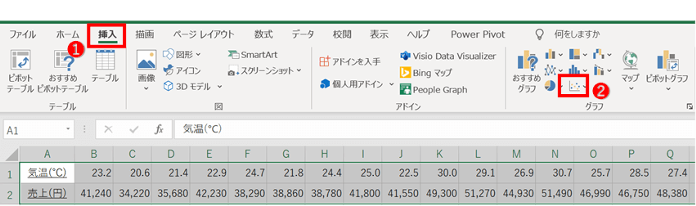
（２）散布図の作成

準備したデータを選択し、メニューバーの「挿入」をクリックし、「グラフ」から「散布図」を選択します。

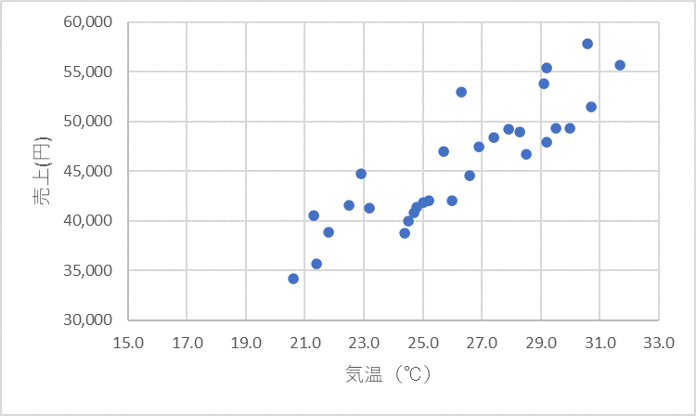
すると、２つのデータの関係性を示す以下のようなグラフが表示されます。

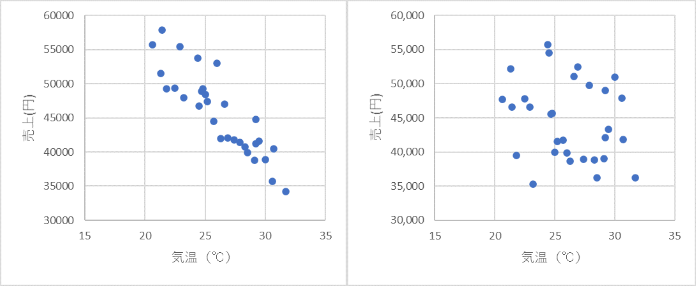
データ内容によっては、上図のような正の相関関係が見えるものもあれば、以下のように負の相関関係（左図）や無相関（右図）などをグラフによって視覚的に理解することができます。

（３）近似曲線の追加

視覚化の最後のプロセスは、「近似曲線の追加」です。近似曲線とは、実際のデータとの誤差が最も小さくなるように引いた曲線（直線）のことです。

具体的な手順は以下の通りです。

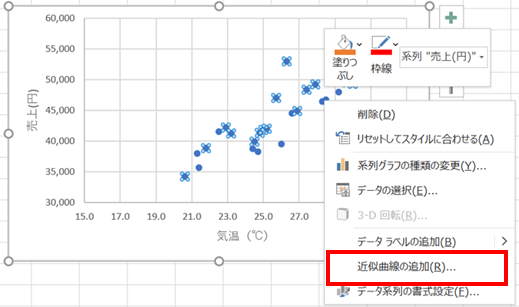
①散布図にプロットされた点を右クリックし「近似曲線の追加」を選択します。出てくる近似曲線のうち「線形近似」を選択します。

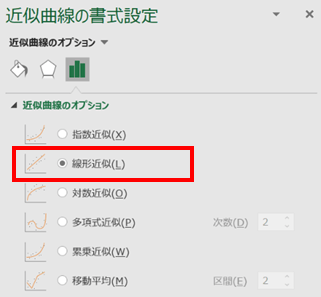
②次に、「近似曲線の書式設定」から、「グラフに数式を表示する」「グラフにR-2乗値を表示する」といったチェックボックスを選択します。

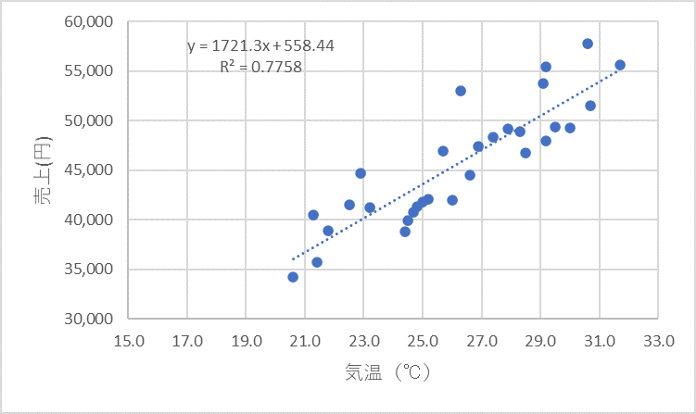
最終的には、右上図のような形で散布図に近似式とR²乗値が表示されます。
「R²乗値」とは「決定係数」とも呼ばれます。「決定係数」は０～１の間の数字を取り、数字が大きければ大きいほど、説明変数が目的変数をどれだけ説明できているかを表します。使用する目的にもよりますが、目安としては0.８以上あれば非常に精度が高く、0.5以上あれば精度としては悪くないと言われています。

３．単回帰分析STEP2：単回帰分析でデータを記述する～回帰式の推定～

続いて、「データ分析」機能を用いて単回帰分析を行ってみましょう。2つの変数間の関係性について、より詳細に把握することができます。把握した内容から予測のモデルを作ります。
　
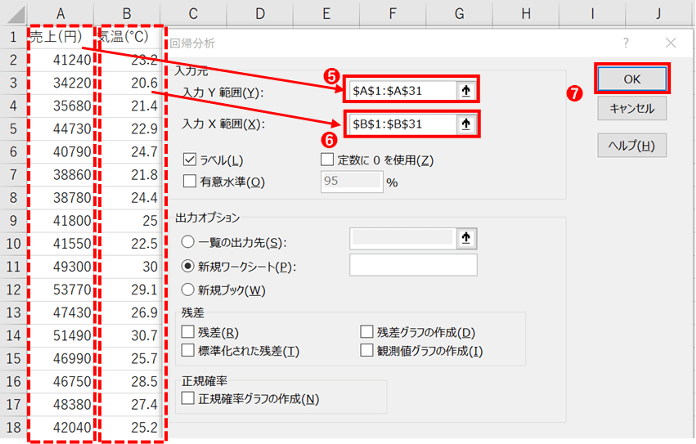
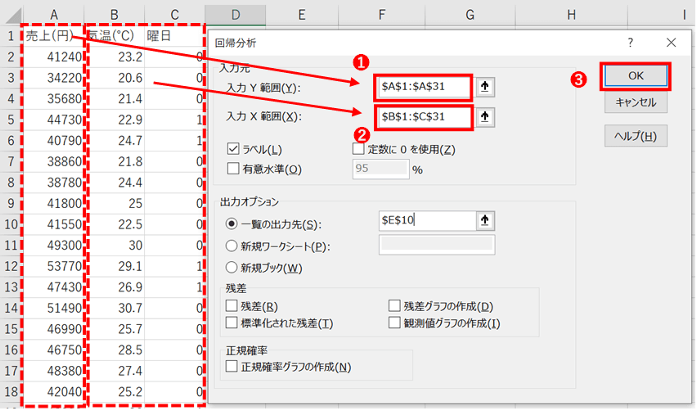
まず、「データ」タブの「データ分析」をクリックし、表示されるポップアップから「回帰分析」を選択します。

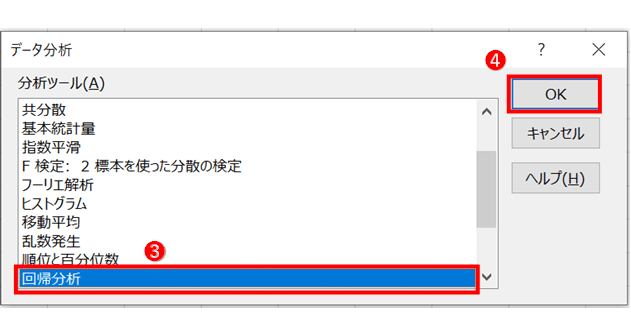
分析したいデータのうち目的変数を入力元の「入力Y範囲」へ、説明変数を入力元の「入力X範囲」へ入力し、「OK」ボタンをクリックします。

すると、以下のような単回帰分析の概要が示されます。

特に注目したいのは、説明変数の係数（回帰係数と言います）とP値です。説明変数の係数は、説明変数が１単位増えると目的変数がどれだけ変わるかを示しています。先ほどの近似曲線で言えば、「傾き」に相当します。P値とは、偶然に起きる確率のようなものと理解いただければと思います。

以下の例では、ほぼ0となっていますので、回帰係数が1721.30909は偶然ではなく、明らかにその傾向があると評価できます。一方、切片（気温が0℃の時の売上）は0.9045となっており、ほぼあてにならないことがわかります。

近似曲線から売上と気温の間には、

予測売上高：y（円）　＝　気温：ｘ（℃）　×　1721.3　＋　558.44

の関係性があり、決定係数が0.776と非常に精度高く説明できることがわかっていました。

また、上記の単回帰分析により、1721.3という傾きは偶然には起こりえない数字である一方、説明変数（気温）が0近い場合上記の式はあてにできないと解釈できます。

近似曲線と単回帰分析から、説明変数（気温）が元データに存在する範囲（20～30℃）であれば、かなりの精度で予測ができそうだということがわかりました。

４．複数の説明変数からなるモデルを作る～重回帰分析～

前項まで、売上と気温というように目的変数と説明変数が１対１の場合を説明してきましたが、さらに説明変数を増やし精度高く分析する方法はないのでしょうか？
本項では、目的変数に対して複数の説明変数からなるモデルを解説したいと思います。このような分析を、単回帰分析と対比し重回帰分析と呼びます。

Excelの操作としては、単回帰分析と同様です。

①「データ」タブ→「データ分析」をクリックし、ポップアップ画面から「回帰分析」を選択

②目的変数を入力元の「入力Y範囲」へ、説明変数を入力元の「入力X範囲」へ入力し、「OK」ボタンをクリック

重回帰分析の場合、「入力Ｘ範囲」に複数列のデータを指定することで分析ができます。
なお、以下の例では休日を“１”、平日を“０”と置いた仮の数値（ダミー変数と呼びます）を入力しています。

出てきた分析結果を確認すると以下のようになりました。
　

分析結果の見方も、変数が増えただけで単回帰分析と同様です。

回帰係数（表内「係数」）より、気温が1℃上がるごとに+1645.7円、休日であれば+2431.2円売上が上がることがわかります。またP値はそれぞれ0に近い（通常、0.05未満であれば採用可）ことから、これらの変数を用いても良さそうです。

上記より、　

予測売上高：z（円）　＝　気温：ｘ（℃）　×　1645.7　

＋　曜日：y(休日は1)　×2431.2　＋　1729.5

という予測式が得られました。

また、決定係数（表内「重決定R2」）を見ると、0.81102となっており、気温だけを説明変数とした単回帰分析よりも、精度の高いモデルになっていることがわかります。

５．重回帰分析の注意点～多重共線性・過学習～

重回帰分析を使用する際に、2つの注意点があります。多重共線性と過学習です。

多重共線性とは、複数の説明変数同士の相関が強い際に起こるトラブルで、発生するとモデルが安定しません。例えば、気温によって売り上げが左右する、といったモデルを作成する際に、最高気温と正午の気温の両方を説明変数に採用してしまう場合などに発生します。

説明変数同士の相関が強くないか確認し、相関が強い（目安として0.7以上）場合は、どちらかを説明変数から外したり、説明変数同士を合成し新たな説明変数を作ったりするといった対処が必要となります。
　
過学習とは、多数の説明変数を組み込むことで、現状データへの当てはまりは非常に良いものの、未知のデータがうまく予測できないトラブルのことを言います。決定係数を高くしようとして、説明変数を加えすぎてしまう場合などに起こります。説明変数を増やしても少ししか決定係数が上がらないような場合には、説明変数を減らすといった対処が必要になります。（専門的には、AICなどを用いしてモデルの評価する必要があります）

６．まとめ

いかがでしたでしょうか？

回帰分析といったやや専門的な分析も、Excelの既存ツールを使えば簡単にできることがわかりました。今回は、回帰分析を活用して売上予測の精度を向上させるといったテーマで解説しましたが、売上予測に限らず、ある変数とある変数の関係性に着目しその関係性を定量的に分析したい場合に使えるツールとなりますので、ぜひ活用してみてください。