Excelで簡単データサイエンス③「打ち手は本当に効果的？」

１．打ち手の効果検証には「検定」を使う

経営を行う上で何かしらの施策を行ったケースを考えてみます。

例えば、売上を向上させるためにチラシ配りをしたとしましょう。チラシを配った日はチラシを配らなかった日に対して、平均で2万円ほど多く売り上げました。この場合は、チラシ配りの効果はあったのでしょうか？

販促担当者は、「平均で2万円多く売り上げたのだから、チラシ配りのコストを考えても効果はあったのだ」と主張しています。

一方で経理担当者は、「売上には日ごとのばらつきがあり、２万円は誤差の範囲だから判断には時期尚早ではないか」と主張しています。

この場合、どちらの意見が正しいのでしょうか？
このようなケースにおいて効果を検証するためには、『検定』が有効です。検定とは、得られたデータから考えた仮説の正しさを統計的に考察することです。検定により、偶然なのか、それとも何らかの意味があったのかを統計的に評価することができます。

２．t検定STEP1：データを視覚化する～箱ひげ図を作成～

「検定」にはいくつかの種類がありますが、今回のように２つのグループの平均に差があるかどうかを調べるといったケースでは、t検定が活用できます。t検定は第２回で紹介した回帰分析と同様、「データ分析」の機能を活用し分析を行うことができます。
データを視覚的に把握することで概要を視覚的にイメージすることができますので、まずはデータを視覚化することから始めましょう。

（１） 箱ひげ図とは

条件の異なる２つのデータの平均の大小を比較するには、「箱ひげ図」を活用します。

数量の大小を比較する際には棒グラフを使用するのが一般的ですが、平均の大小に意味があったかどうかを判断するためには、データがどのようにばらついているのか、その上で平均の差がどの程度あるのかが判断の基準となってきます。

そのため、平均値だけを比較する棒グラフではなく、データの範囲も表す「箱ひげ図」を使用することをお勧めします。

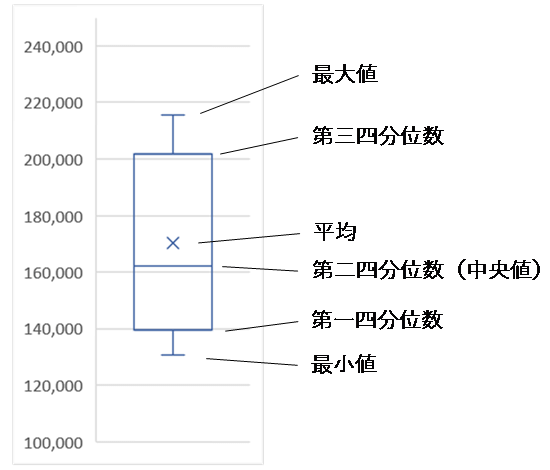
箱ひげ図とは、データの最小値・第一四分位数・第二四分位数・第三四分位数・最大値をグラフで表現したものです。なお、四分位数とはデータを並べた際に小さいほうから25%ずつで区切った数値のことです。第一四分位数は最小値から数えて25%の位置にある数字、第二四分位数は50%の位置にある数字（つまり中央値）、第三四分位数は75%の位置にある数字を表します。

箱ひげ図は以下の図のように、最大値・最小値を「ひげ」で表現し、最小値から数えてデータの範囲が25%～75%の範囲、つまり第一四分位数から第三四分位数の範囲を「箱」で表現したものとなります。また、平均はグラフ内の×印で表現されます。

（２） 箱ひげ図の作成

まず、Excel上に平均を比較したい２つのデータをプロットしたデータファイルを作成します。

準備したデータを選択し、メニューバーの「挿入」をクリックし、次の画像の②で示された「グラフ」の右下のマークをクリックします。

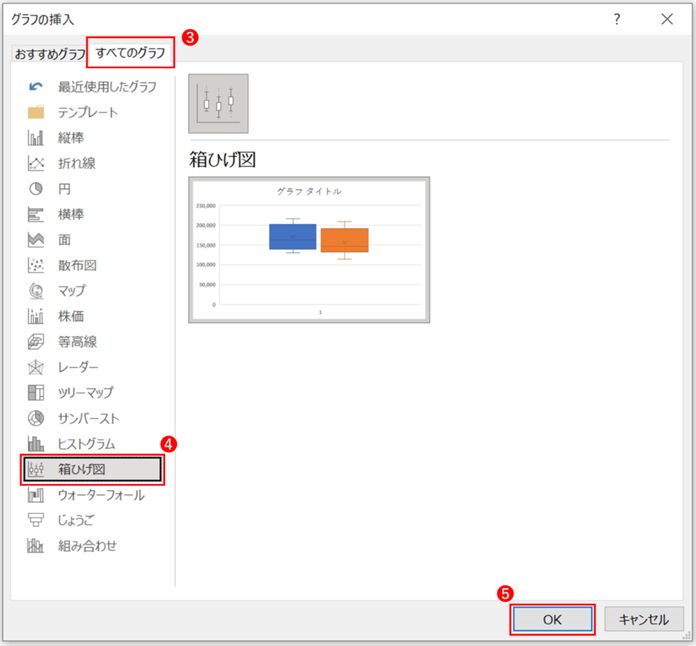
表示されるポップアップの「すべてのグラフ」から「箱ひげ図」を選択します。

すると、２つのデータの箱ひげ図が表示されます。

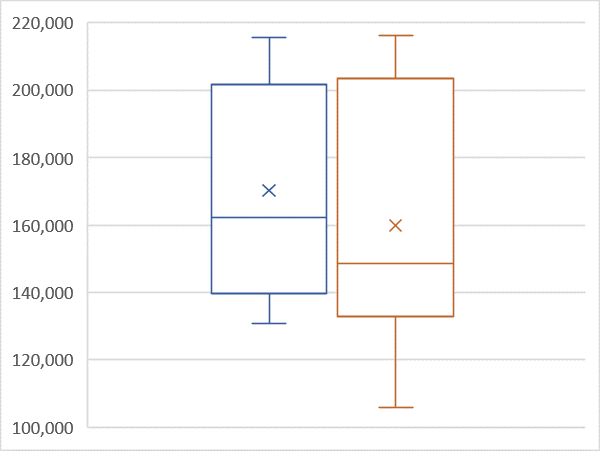
確かに、×印で表現される平均は、チラシなし（右図）に比べてチラシあり（左図）のほうが高くなっていることがわかります。

一方で、両図ともに最大値や第三四分位数はほぼ同じくらいの数値となっていることから、チラシなし（右図）は売上が極端に低い日があり、ばらつきが大きいことで平均が下がってしまっているということが視覚的にわかります。

３．t検定STEP2：t検定で両者の差が偶然か調べる

続いて、「データ分析」機能を用いてt検定を行ってみましょう。

これにより、2つの変数間の平均の差が偶然なのか、それとも意味があるものなのかについて、統計的に把握することができます。
　
まず、「データ」タブの「データ分析」をクリックします。

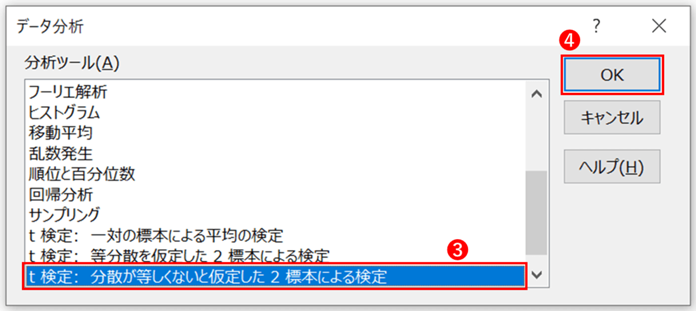
表示されるポップアップから「t検定：分散が等しくないと仮定した2標本による検定」を選択し、「OK」をクリックします。

なお、「データ分析」には、

• 「t検定：一対の標本による平均の検定」
• 「t検定：等分散を仮定した２標本による検定」
• 「t検定：分散が等しくないと仮定した2標本による検定」

の3種類のt検定が準備されています。

同じ人やもので2回計測したデータの差を評価する場合は、「t検定：一対の標本による平均の検定」を使用します。そうでない場合は、「t検定：分散が等しくないと仮定した2標本による検定」を使用します。

「t検定：等分散を仮定した２標本による検定」は、データの分散が明らかになっており分散が同一の場合に使用しますが、事前に分散が明らかになっている場合はまれですので、ほとんど使用しません。

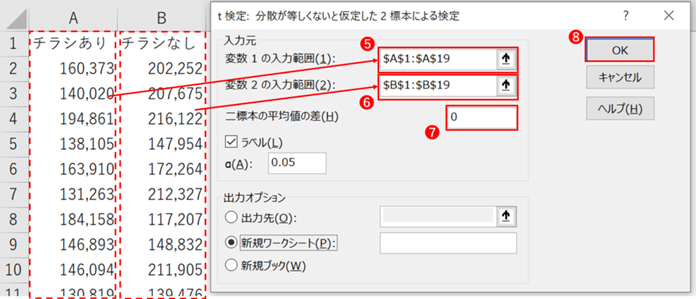
「t検定：分散が等しくないと仮定した2標本による検定」を選択し、「OK」を押すと以下のようなデータ入力画面が表示されます。

分析したいデータをそれぞれ「変数1の入力範囲」と「変数2の入力範囲」へ入力し、「OK」ボタンをクリックします。今回は、二つの標本の平均値の差があるか、ないかを調べますので、➐では0を入力します。

すると、以下のようなt検定の概要が示されます。

t検定では、「両者の平均に差がないという仮説をいったん立て、その仮説が棄却できるかどうか」といった視点で判断します。

以下の概要で表されるP値は、本当は両者の平均が同一である場合でもこのような平均の差が偶然に生まれてしまう確率を表しています。以下の例では、P値が0.361となっていますので、偶然に平均の差が生じてしまった確率が36%あるということを示しています。5%未満である場合、意味のある差異とみなすのが一般的です。

従って、5%を大きく上回った36%である今回は、両者の平均が生じたのはチラシによって生じたものではなく「偶然の域を出ていない」と評価されます。

施策の有無によって売上に意味のある差が生じている、と言い切ることができれば、予算を投入し本格実施することで売上向上につなげることができるでしょう。

一方で、今回のケースのように両者の差が偶然の域を出ない中で、本格的に多額の予算を投入するのはリスクが高いと言えます。統計的に意味のある差と評価できないうちは、試験的に施策を継続するなど慎重な判断が求められます。

なお、今回のケースのように両者の平均の差が意味のあるものと認められない場合でも、「意味がない」とまでは言い切れないことには注意が必要です。意味がないとは言い切れない今回のような場合には、継続的なデータ習得や追加の評価が求められることとなります。

４．まとめ

いかがでしたでしょうか？

施策の効果が出ているか出ていないかについての統計的な判断も、Excelの既存ツールを使えば簡単にできることがわかりました。「勘」や「声の大きい人の意見」に流されることなく統計的に判断することで、より冷静な判断を行うことができます。

全３回の連載では、Excelの既存機能を使い基礎的なデータサイエンスを実践いただく方法を解説してきました。本連載で紹介してきた機能以外にも多数の機能を備えていますので、ぜひ活用してみてください。変化の激しい時代を生き抜くためにも、データを有効に使い価値へつなげていくデータサイエンスを実践してみてはいかがでしょうか。